20 DE ABRIL DE 2017 - 14h00
CAN IMAGE NEGATE?
by Maria Giulia Dondero University of Liège, Belgium

Sala 107, IFCS - UFRJ
That's not an easy question because we need to know exactly what is the basic set up. What does "negate" mean? And what is an image? There is a huge variety of images: photographs, paintings, advertisements, etc. In this talk we will try to answer these questions, facing the ontological status of images.
**************************************************************
29 DE SETEMBRO DE 2016 - 16h30
CONTRADICTION IN QUANTUM MECHANICS?
by Jose Acacio de Barros San Francisco State University

Sala Celso Lemos, IFCS - UFRJ
It is often said that contradictions arise from superpositions of states describing a quantum system, the so called entangled states. However, we will discuss contradictions that come from the mathematical structure of quantum observables, and do not envolve entanglement. This suggests that quantum contradictions arise from mislabeling of empirically observable quantities, and that possible extensions of the quantum formalism may eliminate such contradictions. .
**************************************************************
1 DE JUNHO DE 2016 - 11h00
AS LOGICAS DAS PESSOAS: DOS SONHOS AO CORPO
by Ricardo Kubrusly - UFRJ

Sala 113, IFCS - UFRJ
Primeiro olharemos o nascimento dos princípios clássicos da Logica como determinado pelo corpo do infante que nasce e cresce no mundo.
Depois olharemos as lógicas dos sonhos e como passamos delas para a lógica dos despertos a qual carregamos conosco pelo dia a fora.
Acordar é, nessa visão, o ato de "assinar" um acordo com a Lógica.
**************************************************************
24 DE SETEMBRO DE 2014 17h00
“Der Läufer darf gerade ziehen und der Läufer darf nicht gerade ziehen“: Sketches for an anthropological philosophy of paraconsistency based on the notion of rules
by Marcos Silva
Fedreral University of Ceara, Brazil

Sala 317, IFCS - UFRJ
In Grundgesezte II, Frege (1903) incidentally uses the notion of conflict of rules (“Widerstreit der Regeln”) to understand what contradictions are, when he is critically evaluating some formalist accounts of mathematical practices and entities. In 1930, when Wittgenstein was preparing Waismann for representing him in a very influential panel on Philosophy of Mathematics in to be held in Königsberg, he explicitly borrows from Frege’s discussions this notion of conflict of rules to criticize Hilbert’s metamathematical enterprise. Due to these discussions with members of Vienna Circle (1929-1932), some authors suggest that Wittgenstein could be held as a forerunner of paraconsistent logics. Indeed, Wittgenstein, during these discussions and in other texts from this period, reacts very tolerantly to some non-classical reasoning, especially in the presence of formal contradictions. In this talk, we will not engage in the evaluation of Wittgenstein being a real forerunner for some non-explosive logics, but rather we will investigate why and how the notion of rules in a game could be a seminal philosophical alternative to understand the nature of contradictions without appealing to dialetheias. In the beginning of the 30’s, Wittgenstein’s focus was neither on formal trivialization nor on any mandatory collapse of calculi which entail contradictions, but rather he was already sketching a comprehensive anthropological account of logic. This account may help us to articulate, through the notion of normativity and rules, the nature of formal systems and the relevance of human practices in the construction of both paracomplete and paraconsistent logics.
**************************************************************
02 DE JUNHO DE 2014 15h00
TOWARDS A MULTIFARIOUS QUALITATIVE ABALYSIS OF UNCERZAINITY IN REASONING
by Ivan Varzinczak
Departamento de Ciência da Computação - Instituto de Matemática
Universidade Federal do Rio de Janeiro

Sala do PPGF, IFCS - UFRJ
he last few decades have seen the development of a whole variety of logics, extending or modifying classical logic to deal with many different notions and problems, motivated by philosophical as well as practical needs. These involve different modes of reasoning such as reasoning with uncertainty, exceptions, similarity, vagueness, incomplete information and many others, usually referred to as qualitative uncertain reasoning (or, more commonly, nonmonotonic reasoning). Notwithstanding all the progress that has been achieved, some important facets of nonmonotonicity in logic have largely been overlooked or have only been partially treated so far. To witness, the literature on nonmonotonic reasoning has focused almost exclusively on nonmonotonicity of conditional forms; the question as to which notions of nonmonotonic entailment are most appropriate in given contexts remains open, and belief revision paradigms are largely restricted to an underlying classical (Tarskian) consequence relation. Moreover, well-established approaches are largely based on propositional languages or haunted by the undecidability of full first-order logic. Modern applications require formalisms with a good balance between expressive power and computational complexity. Even if some of the issues related to uncertainty in reasoning have been studied using probabilistic approaches and statistical methods, their qualitative computational nature remains a large avenue for exploration. Therefore, there is a need to investigate and design new general logical methods with which one can better understand, formalize and get to grips with the different aspects of nonmonotonicity in reasoning at all its different levels. In this talk we shall (i) attempt to depict a coherent picture of qualitative uncertain reasoning in all its forms; (ii) give an overview of our recent contributions towards such a unifying theory, and (iii) provide directions for further exploring the questions that still remain open.
**************************************************************
28 DE ABRIL DE 2014 15h00
CONSERVATIVITY OF LOGICAL EXTENSIONS VIA REFLECTIVE TRANSLATIONS
by Sérgio Marcelino
joint work with Carlos Caleiro SQIG - Instituto de Telecomunicacões
Dep. Mathematics, IST - TU Lisbon, Portugal
Sala do PPGF, IFCS - UFRJ
Given two Tarskian consequence relations ⊢ over the language L
and ⊢' over the language L', we say that ⊢ extends ⊢' , if L' ⊆ L and ⊢' ⊆ ⊢. This extension is conservative if for formulas T, a ⊆ L' , T ⊢ a iff T ⊢' a. Consider the concept of sound reflective translations between ⊢ and ⊢' : a function t : L ---> L' s.t. t(T) ⊢' t(a) whenever T ⊢ a and s.t. the restriction of t to L' is the identity function. It easily follows that if ⊢ extends ⊢' and there is such t
between them, then this extension is conservative. Hence a possible method
to prove conservativity of logical extensions is to find such translations. We present some applications of this method, most notably we generalize the result for fusion of modal logics for many cases when the base propositional logic is subclassical, and obtain an alternative proof for the full result for classically based modal logics using only syntactic reasoning.
**************************************************************
28 DE MARCO DE 2014 17h00
Lançamento da edição bilingue de Da Interpretação de Aristóteles apresentada e traduzida por José Veríssimo Teixeira da Mata, UNESP, 2013
seguido da palestra:
DA INTERPRETACAO: ESTRUTURA, FUNCAO E PERMANENCIA
José Veríssimo Teixeira da Mata
Cãmara dos Deputados, Brasilia
Sala do PPGF - IFCS - UFRJ
Será feita uma apresentação do texto, da sua função
dentro do pensamento de Aristóteles, de sua posição
dentro desse pensamento e também serão apresentados
alguns elementos para se entender a permanência do texto.
Por que esse texto é um clássico?
Buscar-se-á compreender a diferença entre lógica e teoria
da lógica a partir já dos elementos postos no Da Interpretação.
**************************************************************
25 DE NOVEMBRO DE 2013 14h00
TOWARDS AN ENCYCLOPAEDIA OF LOGIC
by Jean-Yves Beziau
UFRJ, CNPq and ABF

Sala 423, IFCS - UFRJ
I will explain the present project I am working on: to develop the first ever encyclopaedia of logic. I will explain why it is useful, what will be the contents, organization and architecture, discussing encyclopedic projects such as Diderot D'Alembert Encyclopédie and Wikipedia.
***************************************************************
12 DE ABRIL DE 2013 17h00
POLISH SCHOOL OF LOGICAL PHILOSOPHY
by Katarzyna Gan
Jagellionian University, Kraków, Poland

PPGF, IFCS - UFRJ
The aim of my talk is to present Polish logical philosophy in 20th Cenutry, i.e. the legacy of Kazimierz Twardowski – the founder of so-called Lvov-Warsaw School. Among his most renowned disciples are logicians and philosophers as: Stanislaw Lesniewski, Jan Lukasiewicz, Kazimierz Ajdukiewicz, Alfred Tarski, Roman Suszko. One of the most important characteristics of the Lvov-Warsaw School consists in the application of formal methods to solving philosophical problems. This approach is most original in the context of the opposition between the analytical and continental traditions.
**************************************************************
25 DE MARCO DE 2013 10h00
THE METAPHYSICS AND THE SECULARIZATION OF TRUTH TABLES
by Marcos Silva
Federal University of Ceara, Brazil

Sala 301, IFCS - UFRJ
Nowadays, truth tables are lay tools widely used in our manuals for
propositional calculi. But when we deal with such tools in a “secularized
way”, we often do not see that we are working with the assets of a failure,
i.e., we are moving through the assets, the material goods, of a failed
metaphysical system. My aim is to show the central role and limits of the
truth tables in the Wittgenstein´s Tractatus as a special notation to
reveal the essence of language and to avoid absurdities. Here I shall
access a Lebnizian intuition: a project to develop the attractive picture
of a logic completely combinatorial, syntactical and neutral. This reflects
on the ideal that an alleged language´s profound syntax must be
systematically reflected by a perspicuous notation, in such a way that
nonsensical constructions should be avoided by a simple inspection of this
notation. Our symbols can be rather firm threads to the inner side or
essence of things than inevitable obstacles to it. We can see then, in one
turn, several tractarian theses and presuppositions (both metaphysical and
operational) that are concentrated and evident in our current-day use of
the truth table notation, although we do not notice it. On the other hand,
we can also see the tractarian failures, i.e., its deficiencies of
expressibility. We can thus affirm that the *Tractatus* fails where the
truth table notation fails. As a result, we may support the thought that
even when metaphysics is wrong, it can, however, be seminal.
**************************************************************
28 DE JANEIRO DE 2013 10h00
EMPATHY AND TRANSCENDENCE
- REFLEXIONS ON QUINE´S PHILOSOPHY
by Vera Vidal
DEPES/COC/FIOCRUZ-RJ, Brazil

Sala 301, IFCS - UFRJ
The aim of my speech is to show some of my contributions to the exegesis of Quine´s philosophy, emphasizing the role played by notions such as empathy and transcendence in his philosophical system. I hold that Quine is a rigorous systematic philosopher and that, in order to understand each one of his theses and critiques we need to analyse them within the totality of his philosophical investigations. I believe that his system derives from what I call his epistemological project and that all his philosophical theses are founded in his theory of language learning. I also maintain that Quine ´s philosophy shows a very strong pragmatic aspect more closely related to Wittgenstein´s tradition with which Quine is often associated.
****************************************************
23 DE AGOSTO DE 2012 13h00
Who is afraid of Categorical Models?
by Valeria de Paiva
University of Birmingham, UK

Abstract: Categorical Proof Theory scares many logicians. This talk will be a light and hopefully entertaining introduction to categorical proof theory, in particular to categorical models of Linear Logic, oriented towards logicians, interested in proof theory, algebra and linear logic, but not necessarily experts in any of these.
The survey will not go deeply into the details of de?nitions and proofs, it will focus instead on intuitive explanations of why categorical proof theory is nice, which choices can be made and consequences of these. The main issue is the modelling of the operator $!$ ("of course") which can be tackled in many different ways.
There is a paper Categorical Semantics of Linear Logic for All discussing the issue, available here.
Sala 208L Edificio Cardeal Leme, PUC
Como chegar lá
*************************************
18 DE JUNHO DE 2012 14h00
The Hexagon of Opposition:
what it is and how to use it
by Jean-Yves Beziau
IFCS- UFRJ
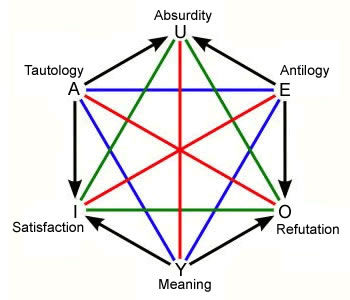
Abstract: The hexagon of opposotion is a generalization of the square of oppositon. In this talk I will first discuss the abstract logical structure of the hexagon. In a second part I will discuss different applications of the hexagon ranging from metalogic to music, through semiotics, economy and cutlery.
Sala de Seminários, Dpto de Análise, Instituto de Matemática e Estatistica da UFF, Niteroi, 4 andar
Como chegar lá
************************************
07 DE MAIO DE 2012 14h00
The story of modern metamathematics
and some recent results
by Andrey Bovykin
University of Bristol, UK/ and UFRJ

Abstract: The story of modern metamathematics started in 1976 with the emergence of (the early versions of) the Paris-Harrington Principle and Friedman's successful initiation of the Reverse Mathematics Programme. Since that time, three generations of dramatical and conflicting metamathematical ideas emerged, including the crisis of 1985 - 1989, when most researchers left the field in pessimism or dispair.
In the first half of the talk I will sketch the history of metamathematics and a kaleidoscope of old (20th century, now outdated) ideas, and the new promising ideas, intuitions, programmes and methods, and motivations behind them, including: Harvey Friedman's machinery and results and Andreas Weiermann's programme of finding threshold versions of unprovability results.
In the second half of the talk, I will speak about the new results (and motivations behind them) done by me and my students and collaborators (mostly Michiel De Smet and Zachiri McKenzie), and the bigger programmes that guide these investigations: the search for Arithmetical Splitting, the study of the Atlas of All Possibilities, the search for the 'true reasons´ for unprovability, the notion of 'wrapping´ axiom schemes, and some Infinite-Dimensional Ramsey Theory.
I will also mention how metamathematical developments since 1976 affected philosophy of mathematics.
The talk will be very simple and accessible to everyone interested in Unprovability.
COPPE
Centro de Tecnologia
Bloco F sala F110- UFRJ
*****************************************
02 DE ABRIL DE 2012 15h00
From contingency to necessity
in modal propositional logic
by Claudio Pizzi
University of Siena, Italy

Abstract: Three notions of contingency have been used in logical and philosophical
literature: the notion of contingency as non-necessity, the notion of contingency as bilateral possibility, and the notion of “contingently true”.
According to a well-known result due to M. Cresswell, ? Necssity is definable in terms of bilateral possibility only in propositional normal modal systems which are at least as strong as KT, but undefinable in weaker non-pathological normal systems.
The paper aims at proving that the required definition is possible provided that
the language of propositional modal logic is extended with at least a suitably
axiomatized propositional constant. Recent results concerning the properties of
such extended contingential systems and their relations with standard modal
systems are introduced and analytically discussed. ris
Salão Nobre, 2 andar, IFCS - UFRJ
Como chegar lá
*****************************************
12 DE DEZEMBRO DE 2011 14h00
Logic is not logic
by Jean-Yves Beziau
IFCS- UFRJ

Salão Nobre, 2 andar, IFCS - UFRJ
Como chegar lá
Abstract: In this talk, we discuss the difference between logic as reasoning and logic as a theory about reasoning. In the light of this distinction we examine central questions about history, philosophy and the very nature of logic.
We study in which sense we can consider Aristotle as the first logician, Descartes‘s rejection of syllogistic as logical, Boole rather than Frege as the initiator of modern logic.
We examine also in this perspective the unfolding of logic into logic and metalogic, the proliferations of logic systems, the questions of relativity and universality of logic and the position and interaction of logic with regards to other sciences such as physics, biology, mathematics and computer science.
******************************************
Dynamic Modal Logic
Changing Structures
by Raul Fervari
University of Cordoba, Argentina

Sala H-324A - PESC/COPPE -
Programa de Engenharia de Sistemas e Computação
Cidade Universitária, Centro de Tecnologia
Como chegar lá
Abstract: In this talk I will present some modal languages that allows a real dynamic perspective over relational models.
First of all, I will introduce the basic modal logic just to fix some notation, and then I will discuss two languages specially designed to express dynamic properties of models: Memory Logic and Swap Logic.
I will discuss some of the results we have already obtained for these logic as examples of their behavior. In particular I will show that the model checking problem for Memory Logic is PSpace-Complete (i.e., as hard as model checking full first-order logic); and a characterization of Swap Logic as a fragment of First Order Logic.
The general message is that dynamic logics as the ones we presented are very expressive, and that while general techniques can be adapted to treat them, sometimes a new perspective is required.
**********************************
The twofold Church-Turing Thesis : a research program
by Maël Pégny,
Université Paris 1, Panthéon-Sorbonne, France
(Visiting PUC-RJ, CAPES-COFECUB)
Salão Nobre, 2 andar, IFCS - UFRJ
Como chegar lá

Abstract: One can commonly find in the literature two different versions of the Church-Turing Thesis. The first one states that every function calculable by an algorithm is partial recursive; the second that every function calculable by a machine is partial recursive. I will argue that these two forms of the Church-Turing Thesis should be carefully distinguished, and that the study of their relation is a well-defined research program, with rich implications for philosophy, physics and logic.
********************************
6 DE JUNHO DE 2011 14h0o
Sala de Seminários, Dpto de Análise, Instituto de Matemática e Estatistica da UFF, Niteroi
Como chegar lá

First Meeting
Presentation of the members
and organization of the seminar
31 DE OUTUBRO DE 2016 - 10h00
PARACONSISTENCY: AN EPISTEMIC PERSPECTIVE
by Abílio Rodrigues Dept de Filosofia - UFMG

Sala 323, IFCS - UFRJ
The central feature of paraconsistent logic is the rejection of the principle of explosion. This principle, valid in classical logic, allows to conclude anything from a contradiction. For this reason, paraconsistent logic is able to represent argumentative contexts in which contradictions are accepted. The question that immediately arises is the following: what is the nature of these contradictions?
The purpose of this talk is to present an epistemic interpretation of paraconsistency according to which such contradictions are originated in thought and language. This view is opposed to the dialetheist thesis according to which there are true contradictions.
After a discussion of the motivations of the epistemic interpretation, formal systems designed to express preservation of evidence rather than preservation of truth will be presented. The notion of 'evidence for a proposition A' is understood as ' reasons for believing in/accepting A'. Evidence may be contradictory in contexts where there is conflicting but and non-conclusive evidence.
This interpretation of paraconsistency is related to various topics of philosophy of logic, which will also be addressed, namely: the nature of logic, versions of the principle of non-contradiction, logical pluralism, inferential semantics, the duality paraconsistency/intuitionism.
**************************************************************
29 DE SETEMBRO DE 2016 - 16h30
QUANTUM MECHANICS, SUPERPOSITIONS, AND CONTRADICTIONS
by Décio Krause - UFSC

Sala Celso Lemos, IFCS - UFRJ
Some authors have claimed that superpositions may involve contradictions. In this talk I will explain for a wide audience the main concepts involved and argue that this idea involves assumptions that are out of the quantum theory properly speaking.
**************************************************************
20 DE ABRIL DE 2016 11h00
A LOGICA DE APULEIO
by Paulo Alcoforado


Sala Celso Lemos, IFCS - UFRJ
Apuleius (125-170) from Madaurus is famous as the author of the Golden Ass. He was also a major figure in the development of logic, having in particular drawn the first
square of opposition. A general view on Apuleius's contributions to logic will be presented in this talk and the book
A Lógica de Apuleio will be launched. It contains a translation in Portuguese of the main work of Apuleius, De Interpretatione. This is the first book to be released in the book series
Cadernos de Lógica e Filosofia, a series promoting works in philosophical logic in Portuguese.
**************************************************************
24 DE SETEMBRO DE 2014 18h00
TEMPORAL OPERATORS, DOUBLE INDEXING AND EXPRESSIBILITY
by David Rey
Logos, University of Barcelona, Spain, FAPERJ visiting PhD student at PPGF-UFRJ

Sala 317, IFCS - UFRJ
During the 70s there was debate among tense logicians about the expressive power of temporal logic systems. Early in that decade Kamp had argued that double indexing was necessary in order to capture the distinction between ‘would be’ and ‘will be’ constructions in English. Other theorists then argued that two temporal indices were not enough. They claimed that it was possible to find English sentences that can only be formalized in a temporal-logic framework by positing three or more indices in the semantics. The conclusion that emerged from this line of argument was that only a system with infinite temporal indices could have the expressive power of English. Some critics of temporal logic suggested that a system of this kind is problematic because (1) it does not differ substantially from standard quantificational accounts of temporal discourse and (2) it provides ad hoc and inelegant formalizations of natural language sentences. In my talk I will look at this literature with a critical eye. I will argue that the arguments for going beyond double indexing were not really conclusive. The different English sentences that motivated the addition of further indices can actually be formalized in a double-index framework.
**************************************************************
24 DE SETEMBRO DE 2014 19h00
Mudança de Paradigmas na Lógica: Do Mundo Clássico ao Universo Pluralista
by Tony Marmo

Sala 317, IFCS - UFRJ
Um tema significativo na História das Ciências são as mudanças de paradigma, primeiro examinadas por Thomas Kuhn. Em sua obra Sylvain Bromberger, atualmente professor no MIT, ofereceu outro ponto de vista sobre o mesmo tema a partir da sua teoria do conhecimento/ ignorância. Para ele, a investigação científica começa com critérios para solucionar questões, para as quais não há ainda respostas satisfatórias. Mas nisso já há um paradoxo: o pesquisador acredita poder encontrar respostas corretas, sem conhecer de antemão quais seriam, aliás, sem saber se existem mesmo tais respostas. As mudanças de paradigma são mudanças de escolha das questões, mas é preciso esclarecer que critérios pesam na transição entre dois paradigmas. A lógica, enquanto disciplina ou ciência, passou por mais de uma ruptura ao longo do século XX, o que criou uma pluralidade de paradigmas lógicos. Tentaremos, modificando um tanto as ideias de Bromberger, examinar o que aconteceu para haver essa proliferação de paradigmas.
**************************************************************
19 DE MAIO DE 2014 15h00
SHEAVES FOR CHILDREN
by Eduardo Ochs
Departamento de Física e Matemática
Pólo Universitário de Rio das Ostras
Universidade Federal Fluminense

Sala do PPGF, IFCS - UFRJ
First-year university students -- the ``children'' of the title --
often prefer to start from an interesting particular case, and only
then proceed to general statements. How can we make intuitionistic
logic, toposes, and sheaves accessible to them?
Let D be a finite subset of N2. Draw arrows for all the ``black
pawns moves'' between points of D, and let D be the poset
generated by that graph; D is what we call a ``ZDAG'', and SetD is a ``ZDAG-topos''. It turns out that the truth-values
of a SetD can be represented in a very nice way as
two-dimensional ASCII diagrams, and that all the operations leading to
sheaves and geometric morphisms can be understood via algorithms on
diagrams.
In this talk we will present a computer library for performing
computations interactively on the truth-values of ZDAG-toposes. The
diagrams are rendered in ASCII by default, but there is a module that
typesets them in LaTeX.
3 DE FEVEREIRO DE 2014 14h00
TRANSREAL NUMBERS AND THEIR APPLICATIONS IN LOGIC
by Walter Gomide
UFMT, Cuiaba

Sala Celso Gomes, IFCS - UFRJ
Os números transreais foram criados pelo cientista da computação inglês James A.D.W. Anderson, no final do século XX. A novidade introduzida pelos transreais é a divisão por zero.
Basicamente, os transreais consistem em uma extensão dos reais mediante a introdução de três constantes, a saber:
a) 1/0 = 8 (infinito positivo):
b) -1/0 = -8 (infinito negativo);
c) 0/0 = f (nulidade – “nullity”).
O objetivo desta palestra é apresentar, a partir dos números transreais, tanto uma semântica clássica como uma não-clássica a fim de obter um “modelo geométrico” para questões lógicas.
**************************************************************
25 DE MARCO DE 2013 11h00
THE POINT OF AVAKTAVYRAM IN JAIN'S EPISTEMOLOGICAL LOGIC
by Miray Yazgan
University of Istanbul, Turkey

Sala 301, IFCS - UFRJ
The aim of this study is to discuss on Avaktavyam, which is the main subject of the Jain logical system called saptaghangi, in the framework of Jain's Epistemlogical Logic.
Jainism is one of the most important doctrines of Indian philosophy. In this study, which is done in order to explain what Avaktavyam is, the previous studies on Avaktavyam will be taken in hand and then our opinions on the subject will be discussed.
The importance of this study for us is the belief that this study on Jaina and its keystone Avaktavyam will be an important source for us in the future in the field of the studies on comparing philosophical thoughts and logic.
*****************************************************************
22 DE JULHO DE 2013 10h00
THE "LOGIC" OF QUANTUM PHYSICS
by Decio Krause
UFSC, Florianópolis
Sala 113, IFCS - UFRJ
Birkhoff and von Neumann claimed in 1936 that the logic of quantum mechanics would be non-classical, for one of the most basic laws of this logic, namely, the distributive law, would not hold in the quantum realm. Starting mainy in the sixties, a new field of logic arose from this basic insight, the domain of quantum logics. But Birkhoff and von Neumann worked from an algebraic point of view, and the mathematical structure they have enlighten was that of an orthomodular lattice, which corresponds to the lattice of the closed subspaces of a Hilbert space, a basic tool in the quantum formalism. Quantum logics were ever since identified with the study of such a lattice and its variations, and much has been done in this field. But a basic question remained unanswered for a long time. As is well known, classical propositional logic has a Boolean algebra as its Lindenbaum algebra. But now we have an orthomodular lattice, that is, an algebraic structure do deal with. What would be the "logic" (in the sense of a calculus of deductions) which corresponds to this algebraic structure? Several attempts have been made by different authors. In this talk we sketch the problematic and discuss the basic concepts underling this interesting and philosophically motivated topic.
*****************************************************************
27 DE SETEMBRO DE 2012 09h30
Opposition from the viewpoint of Universal Logic
by João Marcos
LoLITA and DIMAp, UFRN, Brazil
Sala 113, IFCS - UFRJ
Negation, denial and refutation are fascinating many-sided operations,
and the Aristotelian Square of Oppositions (SoO) is a well-rounded
diagrammatic endeavor to capture some of their main facets and
interrelationships, for the case of the so-called categorical
propositions. The multiple ways in which a given statement-form can be
countered by another statement-form are usually characterized
semantically, with the help of the two classical logical values, true
and false: for a given n-ary statement ⊚, its contradictory
×⊚ is such that ⊚ and ×⊚ always assume
different truth-values, its subalternate ↓⊚ is such that
it inherits the value of ⊚ in case this value is true, its
contrary ⋏⊚ is such that ⊚ and ⋏⊚ cannot
both be true (but may both be false), its subcontrary ⋎⊚
is such that ⋎⊚ and ⊚ cannot both be false (but may
both be true). Among these operations, subalternation is the only
non-involutive one. It raises in fact several difficult technical
issues in the theory of quantification, and does not seem anyway to
convey any reasonable sense of opposition, to start with. My first
proposal here, thus, is to exchange ↓ by a more general and
involutive duality operator ≀ that does offer a useful
perspective on opposition. Next, I show that contradictoriness and
duality may both be characterized from the point of view of Universal
Logic, using nothing but the abstract theory of (symmetric)
consequence relations, and a side-effect of this is that a genuine
proof-theoretical approach to the SoO is ready at hand. A suitable
combination of × and ≀, as applied to a given node
comprising a statement-form ⊚, may obviously be used to generate
the other nodes of a related SoO. Furthermore, the mentioned universal
approach lifts in a wholly natural way from classical propositional
logic to quantificational, modal or many-valued logic, or to any other
tarskian/scottian logic, irrespective of its circumstantial semantical
characterization. It's not all a geometrical bed of roses for the
universal approach, of course. As it should be expected, some
statement-forms simply do not have contrary or subcontrary
counterparts, and a characterization of the initial semantical ideas
behind ⋏ and ⋎ from the point of view of Universal Logic
is found wanting: for the well-studied unary and the binary cases, the
troubles appear when a given statement-form is self-dual, or when its
dual counterpart is identical to its contradictory counterpart, as
such situations make the square collapse into a line; however, in the
analysis of the generic n-ary case, as I will show, the situation gets
more involved.
.
***************************************************
27 DE SETEMBRO DE 2012 10h30
Multi-dimensional opposition
by Ingolf Max
University of Leipzig, Germany

Abstract: My thesis is that a two-dimensional (in general: an n-dimensional) framework yields a reliable formal representation of the traditional square of opposition. I offer a unifying syntactic approach. This paper consists of two parts:
(1) I introduce some new syntactic tools: variable quantifiers, a new entailment operator and several opposition operators / negations acting on two-dimensional arguments. These new operators are characterized by special reduction rules which allow the interaction of both dimensions. It can be shown that this solution offers a unified and homogeneous representation of the traditional square of opposition.
(2) It will be discussed how this approach contrasts with the approach offered by Fabien Schang and how it can be connected with the approach of using hexagons (Robert Blanché, Jean-Yves Beziau and others).
Sala 113, IFCS - UFRJ
Como chegar lá
******************************************
27 DE SETEMBRO DE 2012 11h30
Potential Knowledge
by André Fuhrmann
University of Frankfurt, Germany

Sala 113, IFCS - UFRJ
We present a notion of being able to phi that is different from the possibility that one phi-s. We argue from the theory of belief revision that believability and knowability are indeed distinct from possible belief or knowledge and offer a new solution to the Fitch-paradox.
****************************************************
30 DE JULHO DE 2012 16h00
The Metaphysics of Non-Individuality
by Decio Krause
UFSC

Abstract: This talk is about metaphysics, quantum metaphysics if we can speak this way. The talk will be quite informal, with instructive pictures and draws to motivate the subjects and a minimal of mathematical equations and concepts. Traditionally, metaphysics (here, freely confounded with ontology) deals with the most general characteristics of being. But in present day philosophy, we should acknowledge that there is no much sense in speculating about the stuff of the world out of considering what science, mainly physics and biology, has to tell us about the issue. And, in doing so, we realize that there are lots of different and non equivalent alternatives for considering the being. Really, we should also acknowledge that there is a sense in saying that any conception of being is linked to a physical theory. We are presently in an era of quite interesting and motivating insights for the metaphysician and for the general philosopher of science, perhaps with no parallel in history. Obviously that we cannot cover all the related topics in this talk, so we have chosen a particular question to be investigated, which perhaps motivate the student to look for more advanced discussions. We deal here with the notion of quantum object, or quanta to simplify. We begin by showing some quite counter-intuitive aspects of quantum theory, focusing on the notions of superposition and entanglement, which are two of the most peculiar traits of quantum physics. After realizing that there are different ways (called “interpretations”) of looking to such phenomena, we discuss the nature of the objects that lie behind these phenomena, which leads us to be realists in a certain sense. By postulating the existence of a certain `object’ behind quantum phenomena, we turn to the discussion about the individuation and identity of such entities, as seen from the point of view of the relevant theories. We comment on the two most historically famous theories about individuation in general, the substratum theories and the bundle of properties theories, and try to apply them to the quantum case, showing the difficulties in each case. We conclude by guessing that a coherent view of quanta as non-individuals go against classical logic and standard mathematics. Then we advance the idea of a metaphysics of non-individuals, of entities devoid of identity conditions, based on an alternative logic-mathematical framework. The details will be explained in the presentation.
Auditório 317, Fundação Getulio Vargas
Praia de Botafogo 190
Como chegar lá
**************************************
18 DE JUNH0 DE 2012 15h00
Wittgenstein, Color and Oppositions
by Marcos Silva
IFCS - UFRJ
Abstract: This work deals with the period of abandonment of the Tractatus. It examines the partial failure of the truth-functional paradigm embodied in the truth table limitations found therein. Viewed rigorously, the truth table’s compositionality as a pattern for analysis was found to be insufficiently comprehensive for the ambitious project of logically analyzing all empirical propositions. This is because of its lack of sensitivity in capturing logical subtleties, such as necessary material truths and contrary propositions arrangements, just as in the paradigmatic case of the ascription of a degree to empirical qualities. This ascription problem was assumed as a general case of the colors exclusion. This shows that there are indeed logical constructions that do not appeal to truth-functions. Some exclusions and implications go un-captured by the truth-functional paradigm with the limit-cases, contradictions and tautologies, the hallmarks of the tractarian logic.
Sala de Seminários, Dpto de Análise, Instituto de Matemática e Estatistica da UFF, Niteroi, 4 andar
Como chegar lá
*****************************************
02 DE ABRIL DE 2012 16h00
The Completeness of Aristotelian Syllogistics
by Pirmin Stekeler-Weithofer
University of Leipzig, Germany

Abstract: Aristotle’s system of deductive forms in the first chapters of his Prior Analytics shows quite surprising insights into the meta-logical status of the relation between different conceptual notions of formal inference. In an implicit answer to Parmenides’ warnings against indirect proofs without checking their admissibility, Aristotle shows the conditions under which we can replace indirect proofs by direct deductions in his system of syllogistic rules with 2 or 3 premises. Indirect proofs use Barbara and Celarent as the only direct rules and derive r from p and q by showing that non-p is inconsistent to p and q. Moreover, Aristotle sketches a proof that shows that the syntactic system of direct syllogistic rules is complete relative to a certain notion of generally valid semantic inferences. The hidden semantic system is a diagrammatic model theory as it was reconstructed by Leonard Euler and as it formally represents all mereological interpretations of the syllogistic formulas.
Salão Nobre, 2 andar, IFCS - UFRJ
Como chegar lá
*****************************************
07 DE NOVEMBRO DE 2011 14h00
Logical abstractions and
logical objects in Frege:
a critical approach
by Matthias Schirn
University of Munich, Germany
Academia Brasileira de Filosofia
Rua Riachuelo 303 - Casa de Osório
Como chegar lá
Abstract: In this talk, I shall critically discuss some key issues related to Frege’s notion of logical object, his paradigms of second-order abstraction principles , his logicism and, if time allows, the position which has come to be known as neo-logicism.
*****************************************
12 DE SETEMBRO DE 2011 14h00
Chaos is undecidable, and other exploits in the realm of an axiomatics for physics
by Francisco Antonio Doria,
Coppe-UFRJ

Academia Brasileira de Filosofia
Rua Riachuelo 303 - Casa de Osório
Como chegar lá
Abstract: We start from Hilbert's 6th Problem and show how to axiomatize large portions of physics (mainly from classical mechanics to first-quantized field theories including general relativity). As an application we show that the axiomatic version of chaos theory is undecidable and incomplete, if consistent. The result is universal, i.e., doesn't depend on the actual way we axiomatize the theories within Zermelo-Fraenkel theory. We also show that computer science cannot be properly axiomatized within Zermelo-Fraenkel set theory.
**********************************
3 DE AGOSTO DE 2011 14h00
Departamento de Filosofia, PUC
Como chegar lá

Aristotle's cubes and first-order quantifiers
by Claudio Pizzi,
University of Siena, Italy
Abstract: A typical feature of so-called "consequential implication" is its basic properties (mainly represented by so-called Aristotle's Thesis ¬(A-->¬A)) can be satisfied by more than one operator. Fot this reason thetraditional Aristotle's square of opposition of implicative statements may be expanded to more complex three-dimensional figures (“Aristotle's cubes”). It is shown that statements of consequential implication may
be translated into special first order statements, so that the traditional square of opposition for quantified statements may be expanded in a parallel way.
***************************************
11 DE JULHO DE 2011 14h00
Sala H-324B - PESC/COPPE -
Programa de Engenharia de Sistemas e Computação
Cidade Universitária, Centro de Tecnologia
Como chegar lá

A graph calculus for proving intuitionistic relation algebraic equations
by Petrucio Viana, IME-UFF
(joint work with Renata de Freitas, IME-UFF)
Abstract: Every relation algebraic (RA) equation E is equivalent to a sentence t(E) of FOL=2R, the first-order language with equality and binary relation predicates. Moreover, all valid inference S |- E, of an RA equation E from a set S of RA equations correspond to the inference of t(E) from t(S) = { t(F) : F in S }. Call a such an inference S |- E intuitionistic if t(E) can be proved intuitionistically from t(S).
We introduce a diagrammatic calculus, based on graphs, for proving the intuitionistic inferences (not involving the identity relation). We show that this graph calculus is sound and complete for the aim it was devised.

